PropEr testing of finite state machines

by Eirini Arvaniti and Kostis Sagonas

In this tutorial we will use PropEr to test a finite state machine specification. The testcases produced using the PropEr fsm library (proper_fsm) are of exactly the same form as the testcases produced using the PropEr statem library (proper_statem). The difference lies in the way the callback modules are specified. Before reading this tutorial, please make sure you have understood the basic concepts of testing stateful systems with PropEr, as described here and here.

PropEr fsm offers a convenient way to test systems exhibiting a finite state machine behaviour. That is, systems that can be modeled as a finite collection of named states and transitions between them. A typical finite state machine representation of a system is the state diagram. PropEr fsm is designed to bring the callback module specification very close to a state diagram.

A finite state machine example

Consider the following state diagram that describes the life of a strange creature that feeds on cheese, grapes and lettuce but never eats the same kind of food on two consecutive days.

State Diagram of creature's behaviour

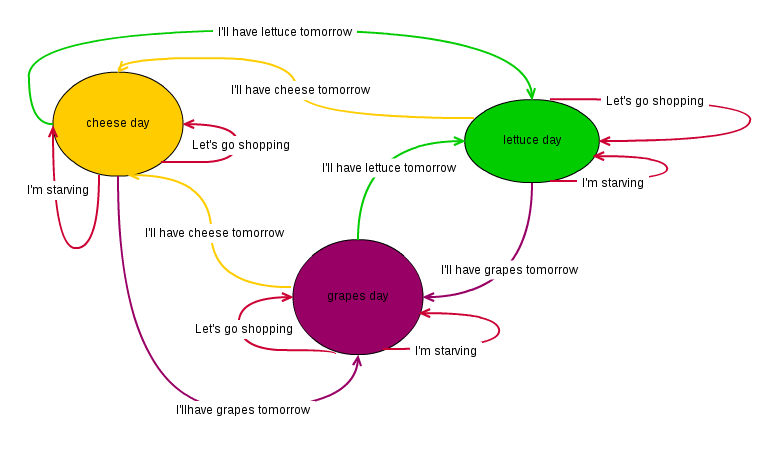
As we can see from the state diagram, days are categorized into cheese_days, lettuce_days and grapes_days. On a cheese_day the creature eats only cheese, on a lettuce_day only lettuce and so on. When it gets hungry, it consumes a fixed portion of the daily food, which is kept in the food storage. To make life less boring and, more importantly, to bring food to the storage, the creature goes shopping from time to time. Finally, every night it decides what to eat the next day. There is only one rule regarding this decision: "never eat the same food for two days in a row".

Being a huge fan of Erlang, this creature has implemented a finite state machine describing its daily routine using the OTP gen_fsm behaviour. The internal state of the finite state machine is a record that represents the food storage. The record fields contain the quantity of food that is currently stored.

-type quantity() :: non_neg_integer().

-record(storage, {cheese  = 5 :: quantity(),
                  lettuce = 5 :: quantity(),
                  grapes  = 5 :: quantity()}).

Let us now describe the API of the finite state machine:

We can start the finite state machine by specifying the kind of day on which it will be started.

-type day() :: 'cheese_day' | 'lettuce_day' | 'grapes_day'.

-spec start(day()) -> {'ok', pid()} | {'error', {'already_started', pid()}}.
start(Day) ->
    gen_fsm:start({local, creature}, ?MODULE, [Day], []).

init([Day]) ->
    {ok, Day, #storage{}}.

We can simulate the condition when the creature is hungry. The function hungry/0 will return us the quantity of available food at the moment when the creature is ready to start eating.

-type food_left() :: 'cheese_left' | 'lettuce_left' | 'grapes_left'.

-spec hungry() -> {food_left(), quantity()}.
hungry() ->
    gen_fsm:sync_send_event(creature, eat).

cheese_day(eat, Caller, #storage{cheese = Cheese} = S) ->
    gen_fsm:reply(Caller, {cheese_left, Cheese}),
    {next_state, cheese_day, S#storage{cheese = Cheese - 1}}.

lettuce_day(eat, Caller, #storage{lettuce = Lettuce} = S) ->
    gen_fsm:reply(Caller, {lettuce_left, Lettuce}),
    {next_state, lettuce_day, S#storage{lettuce = Lettuce - 1}}.

grapes_day(eat, Caller, #storage{grapes = Grapes} = S) ->
    gen_fsm:reply(Caller, {grapes_left, Grapes}),
    {next_state, grapes_day, S#storage{grapes = Grapes - 1}}.

We can simulate the situation when the creature goes shopping to buy some new food.

-spec buy(food(), quantity()) -> 'ok'.
buy(Food, Quantity) ->
    gen_fsm:send_event(creature, {store, Food, Quantity}).

cheese_day({store, Food, Quantity}, S) ->
    case Food of
        cheese ->
            {next_state, cheese_day,
             S#storage{cheese = S#storage.cheese + Quantity}};
        lettuce ->
            {next_state, cheese_day,
             S#storage{lettuce = S#storage.lettuce + Quantity}};
        grapes ->
            {next_state, cheese_day,
             S#storage{grapes = S#storage.grapes + Quantity}}
    end;

lettuce_day({store, Food, Quantity}, S) ->
    case Food of
        cheese ->
            {next_state, lettuce_day,
             S#storage{cheese = S#storage.cheese + Quantity}};
        lettuce ->
            {next_state, lettuce_day,
             S#storage{lettuce = S#storage.lettuce + Quantity}};
        grapes ->
            {next_state, lettuce_day,
             S#storage{grapes = S#storage.grapes + Quantity}}
    end;

grapes_day({store, Food, Quantity}, S) ->
    case Food of
        cheese ->
            {next_state, grapes_day,
             S#storage{cheese = S#storage.cheese + Quantity}};
        lettuce ->
            {next_state, grapes_day,
             S#storage{lettuce = S#storage.lettuce + Quantity}};
        grapes ->
            {next_state, grapes_day,
             S#storage{grapes = S#storage.grapes + Quantity}}
    end;

Note that we will add more clauses to these functions (see below) hence the semicolons at the end of these clauses.

Last but not least, we can simulate the beginning of a new day by specifying the creature's food for that day.

-spec new_day(food()) -> 'ok'.
new_day(Food) ->
    gen_fsm:send_event(creature, {new_day, Food}).

cheese_day({new_day, lettuce}, S) ->
    {next_state, lettuce_day, S};
cheese_day({new_day, grapes}, S) ->
    {next_state, grapes_day, S}.

lettuce_day({new_day, cheese}, S) ->
    {next_state, cheese_day, S};
lettuce_day({new_day, grapes}, S) ->
    {next_state, grapes_day, S}.

grapes_day({new_day, cheese}, S) ->
    {next_state, cheese_day, S};
grapes_day({new_day, lettuce}, S) ->
    {next_state, lettuce_day, S}.

The property to test

Properties for testing finite state machine specifications are very similar to those we have seen in the PropEr statem tutorials. The difference is that the functions commands/1 and run_commands/2 are now imported from proper_fsm module. These functions behave similarly to their proper_statem counterparts, only now commands are generated and executed according to a finite state machine specification.

As a first example, we would like to test that the creature never runs out of food in the storage.

prop_doesnt_run_out_of_supplies() ->
    ?FORALL(Cmds, proper_fsm:commands(?MODULE),
            begin
                start(cheese_day), %% could also be grapes_day or lettuce_day,
                                   %% but the same kind of day should be used
                                   %% to initialize the model state
                {History, State, Result} = proper_fsm:run_commands(?MODULE, Cmds),
                stop(),
                ?WHENFAIL(io:format("History: ~w~nState: ~w\nResult: ~w~n",
                                    [History, State, Result]),
                          Result =:= ok)
            end).

Defining the PropEr finite state machine

State representation

Following the convention used in gen_fsm behaviour, the model state is separated into a state name and some state data. The state name is used to denote a state of the finite state machine and the state data is any relevant information that has to be stored in the model state. States are fully represented as tuples {StateName, StateData}.

Splitting the model state into state name and state data makes the states of the fsm more explicit and allows the specification to be closer to a state diagram of the system under test. The proper_statem:command/1 generator is replaced by a collection of callback functions, one for each reachable state of the fsm. Each callback function is named after the state it represents and takes the state data as argument.

The state is initialized via the initial_state/0 and initial_state_data/0 callbacks. The former specifies the initial state of the finite state machine, while the latter specifies what the state data should initially contain. Let us start on a cheese_day with the default portions of each kind of food available in the storage, since the initial state of our model should coincide with the initial state of the system under test.

initial_state() -> cheese_day.

initial_state_data() -> #storage{}.

Specifying transitions

In our specification, we will define a separate callback function for each state in the state diagram (i.e. cheese_day/1, lettuce_day/1, grapes_day/1). Each of these callbacks should specify a list of possible transitions from that state. A transition is a pair consisting of the target state and the symbolic call that triggers the transition. The atom history can be used as target state to denote that a transition does not change the current state of the fsm.

As we mentioned before, the state callbacks take as argument the state data. In our case, the state data is a record containing the quantity of cheese, lettuce and grapes in the food storage.

cheese_day(_S) ->
    store_transition() ++ eat_transition() ++
        [{grapes_day,  {call,?MODULE,new_day,[grapes]}},
         {lettuce_day, {call,?MODULE,new_day,[lettuce]}}].

lettuce_day(_S) ->
    store_transition() ++ eat_transition() ++
        [{grapes_day, {call,?MODULE,new_day,[grapes]}},
         {cheese_day, {call,?MODULE,new_day,[cheese]}}].

grapes_day(_S) ->
    store_transition() ++ eat_transition() ++
        [{lettuce_day, {call,?MODULE,new_day,[lettuce]}},
         {cheese_day,  {call,?MODULE,new_day,[cheese]}}].

A store_transition is triggered every time the creature buys some food, whereas an eat_transition is triggered every time it is hungry. Both of these transitions do not change the current state of the fsm and this is specified by having history as the target state.

store_transition() ->
    [{history, {call,?MODULE,buy,[food(), quantity()]}}].

eat_transition() ->
    [{history, {call,?MODULE,hungry,[]}}].

We also need to define the generators food() and quantity(). A possible definition of them is given below:

food() ->
    oneof([cheese, lettuce, grapes]).

quantity() ->
    ?SUCHTHAT(I, pos_integer(), I < 5).

Note that we could have defined quantity() more simply as range(1,4). Actually, this would have been a better choice here but, just so as to show how to deal with some possible error situations, let us stick to this definition for the rest of this tutorial.

At command generation time, the callback function corresponding to the current state of the finite state machine will be called to return the list of possible transitions from that state. Then, PropEr will randomly choose a transition and, according to that, generate the next symbolic call to be included in the command sequence. By default transitions are chosen with equal probability, but this behaviour can be fine-tuned, as we will see later.

The other callback functions

Preconditions and postconditions are also imposed on the finite state machine specification. Only now these callbacks take a slightly different form. Instead of the State argument that was provided in proper_statem callbacks, the callbacks in proper_fsm take into account the origin of a transition (From state), the target of a transition (Target state) and the state data.

Initially, let's not have any preconditions.

precondition(_From, _Target, _StateData, {call,_,_,_}) ->
    true.

However, postconditions are needed.

postcondition(cheese_day, _, S, {call,_,hungry,[]}, Result) ->
    Cheese = S#storage.cheese,
    Cheese > 0 andalso Result =:= {cheese_left, Cheese};
postcondition(lettuce_day, _, S, {call,_,hungry,[]}, Result) ->
    Lettuce = S#storage.lettuce,
    Lettuce > 0 andalso Result =:= {lettuce_left, Lettuce};
postcondition(grapes_day, _, S, {call,_,hungry,[]}, Result) ->
    Grapes = S#storage.grapes,
    Grapes > 0 andalso Result =:= {grapes_left, Grapes};
postcondition(_From, _Target, _StateData, {call,_,_,_}, Result) ->
    Result =:= ok.

The set of callback functions corresponding to the states of the fsm update part of the model state, since they specify the target state of a transition. In order to update the state data, we have to define a separate callback function.

next_state_data(_, _, S, _, {call,_,buy,[Food, Quantity]}) ->
    case Food of
        cheese ->
            S#state{cheese = S#state.cheese + Quantity};
        lettuce ->
            S#state{lettuce = S#state.lettuce + Quantity};
        grapes ->
            S#state{grapes = S#state.grapes + Quantity}
    end;
next_state_data(Today, _, S, _, {call,_,hungry,[]}) ->
    case Today of
        cheese_day ->
            S#state{cheese = S#state.cheese - 1};
        lettuce_day ->
            S#state{lettuce = S#state.lettuce - 1};
        grapes_day ->
            S#state{grapes = S#state.grapes - 1}
    end;
next_state_data(_From, _Target, StateData, _Result, {call,_,_,_}) ->
    StateData.

PropEr in action

Let us run the first test on our property. It states that the creature never runs out of food in the storage.

5> proper:quickcheck(food_fsm:prop_doesnt_run_out_of_supplies()).

Error: The transition from "cheese_day" state triggered by
{food_fsm,new_day,1} call leads to multiple target states.
Use the precondition/5 callback to specify which target state should be chosen.
** exception error: too_many_targets

Well, we didn't see that coming! It seems that some part of our specification is not proper enough.

PropEr allows more than one transitions to be triggered by the same symbolic call and lead to different target states. As in this case:

cheese_day(_S) ->
    [{grapes_day,  {call,?MODULE,new_day,[grapes]}},
     {lettuce_day, {call,?MODULE,new_day,[lettuce]}}].

However, the precondition callback may return true for at most one of these target states. Otherwise, PropEr will not be able to detect which transition was chosen and an exception will be raised. In our case, we have to specify the following preconditions to associate each possible argument of new_day/1 with the correct target state.

precondition(Day, Day, _, {call,_,new_day,_}) ->
    false;
precondition(_, grapes_day, _, {call,_,new_day,[grapes]}) ->
    true;
precondition(_, cheese_day, _, {call,_,new_day,[cheese]}) ->
    true;
precondition(_, lettuce_day, _, {call,_,new_day,[lettuce]}) ->
    true;
precondition(_, _, _, {call,_,new_day,_}) ->
    false;
precondition(_, _, _, {call,_,_,_}) ->
    true.

We run the test one more time:

8> proper:quickcheck(food_fsm:prop_doesnt_run_out_of_supplies()).
.................................................
Error: Couldn't produce an instance that satisfies all strict constraints after 50 tries.
{error,cant_generate}

Ooops! Now we have triggered another kind of error. This error suggests that a ?SUCHTHAT constraint could not be satisfied with the default value of 'constraint_tries'. At this point there are two options. We can either increase the constraint_tries limit to e.g. 100 tries by running

proper:quickcheck(food_fsm:prop_never_run_out_of_supplies(), {constraint_tries,100})

or we can modify the generator that is responsible for this error. We choose to take the second option so as to eliminate the error permanently. A ?SUCHTHAT constraint occurs in the quantity/0 generator. It was introduced to control the quantity of food that can be bought in one transaction. The modified generator may return any positive integer after 50 failing attempts to produce a positive integer less than five.

quantity() ->
    ?SUCHTHATMAYBE(I, pos_integer(), I < 5).

And again we run the test:

10> proper:quickcheck(food_fsm:prop_doesnt_run_out_of_supplies()).
.........................................................................
...........................
OK: Passed 100 test(s).

Finally some results! It seems that there is always some food in the storage. But... wait a minute! We cannot be sure of what was tested unless we have a look at the testcase distribution.

prop_doesnt_run_out_of_supplies() ->
    ?FORALL(Cmds, proper_fsm:commands(?MODULE),
            begin
                start(cheese_day), %% could also be grapes_day or lettuce_day,
                                   %% but the same kind of day should be used
                                   %% to initialize the model state
                {History, State, Result} = proper_fsm:run_commands(?MODULE, Cmds),
                stop(),
                ?WHENFAIL(io:format("History: ~w~nState: ~w\nResult: ~w~n",
                                    [History, State, Result]),
                          aggregate(zip(proper_fsm:state_names(History),
                                        command_names(Cmds)),
                          Result =:= ok))
            end).

The property is now instrumented to collect statistics about how often each transition was tested. Let's try it:

12> proper:quickcheck(food_fsm:prop_doesnt_run_out_of_supplies()).
.........................................................................
...........................
OK: Passed 100 test(s).

20% {cheese_day,{food_fsm,new_day,1}}
14% {grapes_day,{food_fsm,new_day,1}}
14% {lettuce_day,{food_fsm,new_day,1}}
 9% {cheese_day,{food_fsm,hungry,0}}
 9% {cheese_day,{food_fsm,buy,2}}
 8% {lettuce_day,{food_fsm,buy,2}}
 8% {grapes_day,{food_fsm,buy,2}}
 7% {grapes_day,{food_fsm,hungry,0}}
 7% {lettuce_day,{food_fsm,hungry,0}}
true

It seems that the creature doesn't get hungry very often in our tests. Thus, our previous conclusion about everlasting food supplies cannot be really trusted. We can instruct PropEr to choose hungry/0 calls more often by assigning weights to transitions. The optional callback weight/3 serves exactly this purpose.

weight(From, Target, Call) assigns an integer weight to transitions from From state to Target state triggered by Call. Each transition is now chosen with probability proportional to the weight assigned.

weight(_Today, _Tomorrow, {call,_,new_day,_}) -> 1;
weight(_Today, _Today, {call,_,hungry,_}) -> 3;
weight(_Today, _Today, {call,_,buy,_}) -> 2.

Running the test with weighted transitions:

15> proper:quickcheck(food_fsm:prop_doesnt_run_out_of_supplies()).
..........................!
Failed: After 27 test(s).
[{set,{var,1},{call,food_fsm,hungry,[]}},
 {set,{var,2},{call,food_fsm,new_day,[grapes]}},
 {set,{var,3},{call,food_fsm,hungry,[]}},
 {set,{var,4},{call,food_fsm,hungry,[]}},
 {set,{var,5},{call,food_fsm,hungry,[]}},
 {set,{var,6},{call,food_fsm,buy,[lettuce,3]}},
 {set,{var,7},{call,food_fsm,hungry,[]}},
 {set,{var,8},{call,food_fsm,hungry,[]}},
 {set,{var,9},{call,food_fsm,hungry,[]}},
 {set,{var,10},{call,food_fsm,buy,[cheese,3]}},
 {set,{var,11},{call,food_fsm,hungry,[]}},
 {set,{var,12},{call,food_fsm,hungry,[]}},
 {set,{var,13},{call,food_fsm,hungry,[]}}]
History: [{{cheese_day,{storage,5,5,5}},{cheese_left,5}},
          {{cheese_day,{storage,4,5,5}},ok},
          {{grapes_day,{storage,4,5,5}},{grapes_left,5}},
          {{grapes_day,{storage,4,5,4}},{grapes_left,4}},
          {{grapes_day,{storage,4,5,3}},{grapes_left,3}},
          {{grapes_day,{storage,4,5,2}},ok},
          {{grapes_day,{storage,4,8,2}},{grapes_left,2}},
          {{grapes_day,{storage,4,8,1}},{grapes_left,1}},
          {{grapes_day,{storage,4,8,0}},{grapes_left,0}}]
State: {grapes_day,{storage,4,8,-1}}
Result: {postcondition,false}

Shrinking .....(5 time(s))
[{set,{var,4},{call,food_fsm,hungry,[]}},
 {set,{var,8},{call,food_fsm,hungry,[]}},
 {set,{var,9},{call,food_fsm,hungry,[]}},
 {set,{var,11},{call,food_fsm,hungry,[]}},
 {set,{var,12},{call,food_fsm,hungry,[]}},
 {set,{var,13},{call,food_fsm,hungry,[]}}]
History: [{{cheese_day,{storage,5,5,5}},{cheese_left,5}},
          {{cheese_day,{storage,4,5,5}},{cheese_left,4}},
          {{cheese_day,{storage,3,5,5}},{cheese_left,3}},
          {{cheese_day,{storage,2,5,5}},{cheese_left,2}},
          {{cheese_day,{storage,1,5,5}},{cheese_left,1}},
          {{cheese_day,{storage,0,5,5}},{cheese_left,0}}]
State: {cheese_day,{storage,-1,5,5}}
Result: {postcondition,false}
false

As we can see now, in case of non-stop eating the creature eventually runs out of food. What is more, the content of the State variable reveals that the quantity of available food starts getting negative values. We will correct the code to prevent this from happening.

cheese_day(eat, Caller, #storage{cheese = Cheese} = S) ->
    gen_fsm:reply(Caller, {cheese_left, Cheese}),
    case Cheese > 0 of
        true ->
            {next_state, cheese_day, S#storage{cheese = Cheese - 1}};
        false ->
            {next_state, cheese_day, S}
    end.

lettuce_day(eat, Caller, #storage{lettuce = Lettuce} = S) ->
    gen_fsm:reply(Caller, {lettuce_left, Lettuce}),
    case Lettuce > 0 of
        true ->
            {next_state, lettuce_day, S#storage{lettuce = Lettuce - 1}};
        false ->
            {next_state, lettuce_day, S}
    end.

grapes_day(eat, Caller, #storage{grapes = Grapes} = S) ->
    gen_fsm:reply(Caller, {grapes_left, Grapes}),
    case Grapes > 0 of
        true ->
            {next_state, grapes_day, S#storage{grapes = Grapes - 1}};
        false ->
            {next_state, grapes_day, S}
    end.

Let us now assume that the creature is wise enough to take care of buying food before it gets hungry. This can be modeled by adding the following precondition.

precondition(Today, _, S, {call,_,hungry,[]}) ->
    case Today of
        cheese_day ->
            S#storage.cheese > 0;
        lettuce_day ->
            S#storage.lettuce > 0;
        grapes_day ->
            S#storage.grapes > 0
    end;

At this point, we would like to mention another, less obvious cause of cant_generate errors: difficult-to-satisfy preconditions. After failing constraint_tries times to generate a symbolic call with a true precondition, PropEr will report a cant_generate error. In our specification, this is not the case. Nevertheless, we can instruct PropEr to choose an eat_transition only when there is food available.

cheese_day(S) ->
    store_transition() ++ eat_transition(S#storage.cheese) ++
        [{grapes_day,  {call,?MODULE,new_day,[grapes]}},
         {lettuce_day, {call,?MODULE,new_day,[lettuce]}}].

lettuce_day(S) ->
    store_transition() ++ eat_transition(S#storage.lettuce) ++
        [{grapes_day, {call,?MODULE,new_day,[grapes]}},
         {cheese_day, {call,?MODULE,new_day,[cheese]}}].

grapes_day(S) ->
    store_transition() ++ eat_transition(S#storage.lettuce) ++
        [{lettuce_day, {call,?MODULE,new_day,[lettuce]}},
         {cheese_day,  {call,?MODULE,new_day,[cheese]}}].

eat_transition(Food_left) ->
    [{history, {call,?MODULE,hungry,[]}} || Food_left > 0].

The property now successfully passes 1000 tests.

18> proper:quickcheck(food_fsm:prop_never_run_out_of_supplies(), 1000).
<...1000 dots...>
OK: Passed 1000 test(s).

19% {cheese_day,{food_fsm,hungry,0}}
13% {cheese_day,{food_fsm,buy,2}}
13% {cheese_day,{food_fsm,new_day,1}}
11% {lettuce_day,{food_fsm,hungry,0}}
11% {grapes_day,{food_fsm,hungry,0}}
 8% {lettuce_day,{food_fsm,new_day,1}}
 8% {grapes_day,{food_fsm,new_day,1}}
 7% {lettuce_day,{food_fsm,buy,2}}
 7% {grapes_day,{food_fsm,buy,2}}
true

You can get the complete final code of this tutorial by clicking on the following link: food_fsm.