PropEr testing with search strategies
Targeted Property-Based Testing
Sometimes random generation of input is not sufficient to find property violations in a reasonable amount of time. PropEr provides an extension to random property-based testing (PBT) called targeted property-based testing that employs a search strategy to guide the input generation towards values that have a higher probability of falsifying a property. To be able to do this, the tester has to however specify a few additional ingredients for their properties such as e.g. a search goal.
In this tutorial, we first show the limitations of random input generation on an example, and then show how PropEr can use the search-strategy guided input generation of targeted PBT to overcome these limitations.
Maze Game
Let us assume that we are implementing a game where the player has to start from an entrance and reach one of the exits of a level. To make the maze game fair and fun we want to test that for all levels of our game at least one exit is reachable from the entrance of the level. The level itself is an area enclosed with walls that can contain other wall obstacles. The player can move in four directions: up, left, down, and right.
Levels are represented as a list of stings:
level(0) -> ["#########", "#X E#", "#########"]; level(1) -> ...
Each # represents a wall, an X an exit, and E the (single) entrance of the
level. In this beginners level, the player can reach the only exit by going left
six times. To access the level data easier, we convert the list of strings into
a map with the function build_level/1. For each position of the level that
contains something interesting we store in the map the type (entrance, exit,
or wall). We additionally store the locations for the entrance and the exits:
1> c(maze_game). {ok,maze_game} 2> maze_game:build_level(maze_game:level(0)). #{entrance => {1,7}, exit => {1,1}, {0,0} => wall, {0,1} => wall, ... {1,0} => wall, {1,1} => exit, {1,7} => entrance, {1,8} => wall, ...}
To test that we can reach the exit from the entrance we generate a path and then calculate where we end up at. Our generator is very simple and looks as follows:
step() -> oneof([left, right, up, down]). path() -> list(step()).
To calculate the final position we implement the function follow_path/3.
If when following the path at some point we reach an exit, we do not proceed
further, and the level is finished successfully. The rest of the path is
ignored. If a step hits into a wall, this step is also ignored.
We can now implement a property to test whether in each of the levels an exit is reachable or not:
prop_exit_unreachable(LevelData) -> Level = build_level(LevelData), #{entrance := Entrance} = Level, ?FORALL(Path, path(), case follow_path(Entrance, Path, Level) of {exited, _} -> false; _ -> true end).
The property is parameterized with the level data so that we can easily test
many different levels. Since we are only interested in whether an exit is
reachable or not, and not which exit is reachable (in the case there are
many exits), we ignore the returned position from follow_path().
Note that we expect this property to be falsifiable if the levels are
created correctly.
3> proper:quickcheck(maze_game:prop_exit_unreachable(maze_game:level(0))). .......................................................! Failed: After 56 test(s). [up,left,left,down,up,left,down,left,down,left,down,up,left,up,down,down,right,left,right] Shrinking ..........(10 time(s)) [left,left,left,left,left,left] false
Looks good so far. PropEr finds a path to the exit in just a few tests and
shrinks this path down to only left steps. Let us now test a more complicated
level, one that also contains some obstacles between the entrance and the exit:
level(1) -> ["######################################################################", "# #", "# E #", "# ##### #", "# ##### #", "# ##### ##### ##### #", "# ##### ##### #", "# ##### ##### #", "# ##### #", "# ##### #", "# ##### #", "# ##### ########## #", "# ##### ########## #", "# ##### ##### ########## #", "# ##### #", "# ##### #", "# ##### #", "# ##### #", "# ##### ##### #", "# ##### #", "# ##### #", "# X #", "# #", "######################################################################"].
Since this level is larger, we increase the amount of tests to one million:
4> proper:quickcheck(maze_game:prop_exit_unreachable(maze_game:level(1)), 1000000). .......................... 1.000.000 dots .......................... OK: Passed 1000000 test(s). true
The property passes, but we can clearly see that there are (easy to follow) paths leading from the entrance to the exit. To further analyze what is going on we record the final positions of our randomly generated sequences of moves reach and build a heatmap:
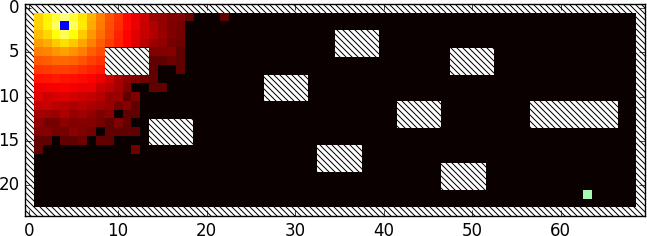
The heatmap shows that the final positions of the paths are concentrated around the entrance. (Actually the final positions are following a normal distribution around the entrance.)
Each step in the path/0 generator is generated randomly and independently
from the other steps in the path. This means that for long paths the steps in
it mostly cancel each other out (e.g., the effect of one step left and one step
right is the same as taking no steps at all). Another issue is that the input
for each test is generated independently from all other tests. This means that
already explored areas are covered again, even if they lead away from the exit.
Ideally we want to learn from the paths that we took before and use this
knowledge to construct a new path that has higher chances of leading us to the
exit.
Targeted Property-Based Testing
PropEr provides an enhanced form of random property-based testing, called targeted property-based testing, where the input generation is not completely random, but instead is guided by a search strategy. The search strategy uses information gathered by previous tests, in the form of utility values, and uses this information in the generation of the next input. The user needs to instruct the search strategy to either maximize or minimize these utility values.
The general structure of a property that can be tested with targeted PBT looks as follows:
prop_Target() -> % Try to check a property ?STRATEGY(SearchStrategy, % for some Search Strategy ?FORALL(Input, ?TARGET(Params), % and for some Parameters begin % for the input generation. UV = SUT:run(Input), % Do so by running SUT with Input ?MAXIMIZE(UV), % and maximize its Utility Value UV < Threshold % up to some Threshold. end)).
The default search strategy of PropEr for targeted PBT is
simulated annealing. To
use this strategy, we can either pass the atom simulated_annealing to the
first argument of the ?STRATEGY macro or, simpler, use the ?FORALL_SA
macro instead of ?STRATEGY(simulated_annealing, ?FORALL(..., ..., ...))
The ?TARGET macro informs PropEr that the generator given in its argument
is under the control of the search strategy. (The Params that are given to
it contain all the information the search strategy needs to generate input for
the property.)
The definitions that are needed here are dependent on the search strategy we
use. For simulated annealing, which is the default search strategy that
targeted property-based testing uses, we need to specify a random generator
for the first element and a neighborhood function. The neighborhood function
should produce a random instance of the input that is similar to (i.e., in the
neighborhood of) a given input instance.
Additionally, we need to tell the search strategy a direction where the
search should be going. This is done by reporting to the search strategy
the utility value of the currently tested input and whether to maximize or
minimize these values with ?MAXIMIZE or ?MINIMIZE. The utility values
capture how close input comes to falsifying the property.
Targeted Testing of Properties
We can use this technique to test the levels of our maze game and improve the chance of finding a path to the exit significantly. We know the location of the exit that we want to reach and the final position of the player when following a path. We can calculate the distance between this final position and the exit:
distance({X1, Y1}, {X2, Y2}) -> math:sqrt(math:pow(X1-X2, 2) + math:pow(Y1-Y2, 2)).
Now we can write prop_targeted_exit_unreachable():
-
We exchange
?FORALLwith?FORALL_SAto use simulated annealing as search strategy. -
We calculate the distance
Dbetween the final player position and the exit and instruct PropEr to minimize this distance with?MINIMIZE(D). -
Finally, we exchange the
path()generator with theTARGET()macro and give it the parameterspath_sa().:::erlang prop_targeted_exit_unreachable(LevelData) -> Level = build_level(LevelData), #{entrance := Entrance} = Level, #{exit := Exit} = Level, ?FORALL_SA(Path, ?TARGET(path_sa()), case follow_path(Entrance, Path, Level) of {exited, _Pos} -> false; Pos -> UV = distance(Pos, Exit), ?MINIMIZE(UV), true end).
For simulated annealing, the parameters in path_sa/0 need to specify a random
generator for the first input and a neighborhood function. The neighborhood
function takes two arguments: (1) the base input and (2) a temperature.
For simplicity, we will initially ignore the temperature parameter.
The neighborhood function should produce a random input that is in the neighborhood of the base input, that is, an input which is similar to the base input. For our path we can just add an extra step. We can use the path generator for the first input:
path_sa() -> #{first => path(), next => path_next()}. path_next() -> fun (OldPath, _) -> ?LET(NextStep, step(), OldPath ++ [NextStep]) end.
If we test this property now it will fail after just a few hundred tests:
5> proper:quickcheck(maze_game:prop_targeted_exit_unreachable(maze_game:level(1)), 1000). -- Simulated Annealing Search Strategy -- Acceptance Function: default Temperature Function: default .................... 326 dots ....................! Failed: After 326 test(s). [up,left,up,down,down,left,up, ...] Shrinking .......................................................................(71 time(s)) [right,right,right,right,right, ...] false
If we produce a heatmap similar to the one for random input generation we can see that the generated paths go towards the exit of the level:
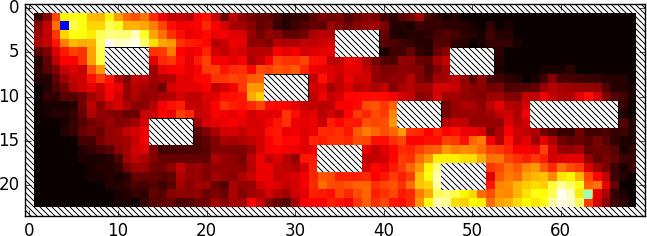
Targeting Performance
Up to now, we are only adding one step at a time for each search step. We can decrease the amount of tests needed by adding lets say 20 steps at a time. If we construct a bad path it will be rejected in the same way, but if we construct a good path we will skip multiple intermediate steps:
path_next() -> fun (PrevPath, _) -> ?LET(NextSteps, vector(20, step()), PrevPath ++ NextSteps) end.
Now the property usually fails in less than 100 tests:
6> proper:quickcheck(maze_game:prop_targeted_exit_unreachable(maze_game:level(1))). -- Simulated Annealing Search Strategy -- Acceptance Function: default Temperature Function: default ..........................................................! Failed: After 59 test(s). [left,up,right, ...] Shrinking .......... ... ..........(100 time(s)) [right,right,right, ...] false
Resetting Bad Runs
With our targeted property in place, we can now try out an even more complicated level, level 2:
level(2) -> ["######################################################################", "# #", "# X #", "# #", "# # ######## ##### #### ######## #", "# ### ## ## # ## # ## #", "################ ## ##### #### ## #", "# ### ## ## ## # ## #", "# # ## ## #### ## #", "# #", "# #", "# # #", "# # #", "# # #################################", "# # #", "# # #", "# # #", "# #################################### #", "# #", "# #", "################################ #", "# E #", "# #", "######################################################################"].
When we test prop_targeted_exit_unreahable() with level 2, we see that
sometimes
the property fails very fast. In other cases however, the property takes many
tests to fail. We can also see that the tests become really slow after a while.
The reason is that we add more and more steps and the path becomes longer with
each test. There are several solutions to this:
- We could write a more complicated neighborhood function that also removes some steps, or one that takes previously visited positions into account when deciding which steps should be taken next. However, we can see that in some cases our existing neighborhood function is sufficient to find the input fast.
- We can reset the search after the path reaches a certain length and start constructing a new path form the entrance.
To help us with our decision, we record the final positions for each generated path for a low amount of tests and accumulate the data over multiple runs. We then build a heatmap from this data:
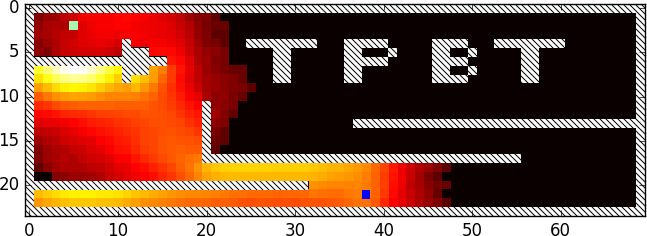
We can see multiple bright spots on the left side and under the arrow. This probably means that the search gets stuck and has a hard time escaping from these areas. We can also see that there are quite a few runs that find the exit. Resetting the search should be sufficient to solve our problem:
prop_targeted_exit_unreachable(LevelData) -> Level = build_level(LevelData), #{entrance := Entrance} = Level, #{exit := Exit} = Level, ?FORALL_SA(Path, ?TARGET(path_sa()), case follow_path(Entrance, Path, Level) of {exited, _Pos} -> false; Pos -> case length(Path) > 500 of true -> proper_sa:reset(), true; false -> UV = distance(Pos, Exit), ?MINIMIZE(UV), true end end).
The function proper_sa:reset/0 discards the current state of the search and
starts from the beginning initial input. If we test the property now, it will
fail after a few thousand tests:
7> proper:quickcheck(maze_game:prop_targeted_exit_unreachable(maze_game:level(2)), 10000). -- Simulated Annealing Search Strategy -- Acceptance Function: default Temperature Function: default ................... 2339 dots ...................! Failed: After 2339 test(s). [down,left,up, ...] Shrinking ...................................................................(67 time(s)) [left,left,up, ...] false
You can get the complete final code of this tutorial by clicking on the following link: maze_game.erl.
